Прямоугольный треугольник
Прямоугольный треугольник: определение. Показываем свойства прямоугольного треугольника. Разбираем примеры практических задач.
Прямоугольный треугольник: определение
Прямоугольным называют треугольник, в котором один из трех углов является прямым, т.е. равным 90°.
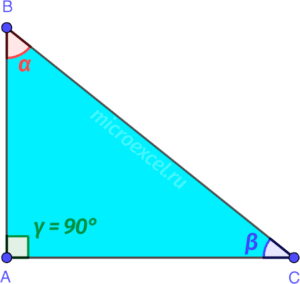
- AB и AC – катеты;
- BC – гипотенуза.
Прямоугольный треугольник может быть равнобедренным – когда оба катета равны, а угол между каждым из них и гипотенузой составляет 45°.

Свойства прямоугольного треугольника
Свойство 1. Сумма двух острых углов прямоугольного треугольника равняется 90°.
α + β = 90°
Сумма всех углов любого треугольника составляет 180°. Т.к. один угол равен 90°, на два других, также, остается 90°.
В нашем случае, катет AB лежит напротив ∠ACB = 30°. Следовательно:
![]()

Обратная формулировка:
Если длина одного из катетов прямоугольного треугольника в два раза меньше длины его гипотенузы, значит угол напротив этого катета равняется 30°.
Свойство 3. Терему Пифагора можно, также, отнести к свойствам прямоугольного треугольника. Согласно ее формулировке, сумма квадратов катетов (a и b) равняется квадрату гипотенузы (c).
a2 + b2 = c2
Таким образом, гипотенуза прямоугольного треугольника больше любого из его катетов.
Свойство 4. Медиана, опущенная на гипотенузу прямоугольного треугольника (проведенная из вершины прямого угла), равняется половине гипотенузы.
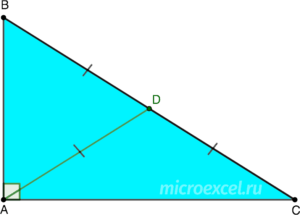
- AD – медиана
- AD = BD = DC
Свойство 5. Середина гипотенузы прямоугольного треугольника – это центр описанной вокруг него окружности.
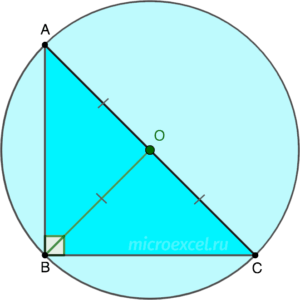
Согласно свойству 4, рассмотренному выше, медиана BO равняется половине гипотенузы AC и, одновременно, радиусу окружности, описанной вокруг △ABC.
