Векторы: мощный инструмент математики и физики в повседневной жизни
Векторы объединяют геометрию и физику, позволяя решать задачи движения, сил и программирования в реальном мире.
Основные свойства векторов: увлекательное описание
Векторы — это не просто математические объекты, которые встречаются в учебниках по алгебре или физике. Они играют ключевую роль в самых разных областях науки и техники, от навигации и компьютерной графики до аэрокосмических технологий. Рассмотрим основные свойства векторов, которые делают их настолько универсальными и полезными.
1. Модуль вектора (длина)
Одно из самых простых свойств вектора — это его длина, или модуль. Если представить вектор как стрелку, направленную в определенную сторону, то длина этой стрелки будет величиной вектора. Длина вектора показывает, насколько “сильно” этот вектор воздействует на объект. Например, если вектор описывает скорость, длина будет соответствовать величине скорости.
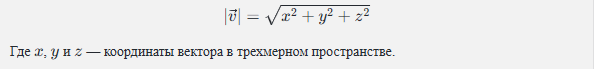
2. Направление вектора
Каждый вектор имеет направление, которое отличает его от скаляров (величин без направления). Представьте себе, что вы бросаете мяч: неважно, с какой силой его бросаете, важно еще и то, в какую сторону. Векторами описываются такие явления, как ветер, перемещение объектов, силы и многие другие процессы, где важен не только размер, но и направление.
3. Сложение и вычитание векторов
Сложение векторов — это одна из самых увлекательных операций. Для наглядности представим два вектора как стрелки, исходящие из одной точки. Чтобы сложить их, нужно поставить конец одного вектора в начало другого. Итоговый вектор будет направлен от начала первого к концу второго. Это называется правилом треугольника. А если складывать несколько векторов, можно представить это как замыкание многоугольника.
Интересный факт: когда в физике складываются силы, это правило треугольника помогает определить результирующую силу на объект!
4. Коммутативное и ассоциативное свойства
Операции сложения векторов обладают коммутативностью, то есть результат не зависит от порядка, в котором вы складываете векторы:
Также, сложение векторов обладает ассоциативным свойством, что значит, что порядок группировки векторов при сложении не влияет на результат:
Это свойство очень полезно в различных вычислениях, как в физике, так и в компьютерной графике, когда требуется сложить множество векторов для моделирования сложных движений или взаимодействий объектов.
5. Умножение вектора на число
Еще одно важное свойство векторов — возможность умножать их на скаляр (обычное число). Если умножить вектор на положительное число, его длина увеличится в это число раз, при этом направление останется прежним. Если умножить на отрицательное число, то вектор поменяет направление на противоположное.
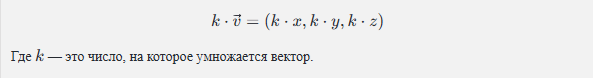
6. Скалярное произведение (dot product)
Скалярное произведение — это операция, при которой два вектора дают в результате скаляр (число). Этот результат зависит как от длины векторов, так и от угла между ними. Скалярное произведение широко используется в физике, например, для вычисления работы силы, когда сила и перемещение объекта не совпадают по направлению.
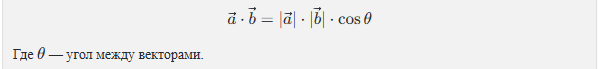
7. Векторное произведение (cross product)
Векторное произведение двух векторов дает новый вектор, перпендикулярный к обоим исходным. Это свойство особенно полезно в физике для вычисления моментов сил или в электромагнетизме.
Длина результирующего вектора зависит от угла между исходными векторами и их длин.
Эти основные свойства векторов делают их мощным инструментом для описания множества явлений в реальном мире. Они помогают нам вычислять скорости, направления, силы, моделировать процессы в физике, навигации и компьютерной графике. Векторы — это не просто абстрактная математика, они лежат в основе многих технологий и приложений, которые мы используем ежедневно.
Где применяются знания о векторах: три ключевые области
1. Векторы в физике и инженерии
В физике и инженерии векторы являются ключевыми инструментами для описания и анализа различных процессов и явлений. Они помогают определить силы, скорости, ускорения и другие физические величины, которые имеют как величину, так и направление. Например, сила, действующая на объект, всегда имеет направление (в сторону действия) и величину (измеряемую в Ньютонах).
Пример: Векторы силы и ускорения
При расчете движения объекта под действием нескольких сил векторы позволяют суммировать эти силы для нахождения результирующего ускорения. Например, если на автомобиль действуют две силы: сила тяги и сила сопротивления воздуха, их можно представить как векторы, которые суммируются для определения итогового ускорения автомобиля.
Пример: Электромагнитные поля
Векторы также используются для описания электрических и магнитных полей, где каждая точка поля может быть описана вектором, указывающим направление силы, действующей на заряженную частицу, и величину этой силы. Это важно при разработке электромагнитных устройств, таких как двигатели или генераторы.
2. Векторы в компьютерной графике и моделировании
Одной из самых наглядных областей применения векторов является компьютерная графика. Векторы играют ключевую роль в создании трёхмерных объектов, анимации и рендеринга изображений.
Пример: Позиционирование объектов в 3D-пространстве
В компьютерной графике каждый объект имеет своё положение в трёхмерном пространстве, которое можно описать вектором. Вектор указывает, где объект находится относительно точки отсчета (например, начало координат). Перемещение объекта в пространстве также описывается изменением его вектора положения.
Пример: Освещение и тени
Векторы используются для расчета направленности света в сцене и взаимодействия света с объектами. Для того чтобы реалистично отобразить тени и отражения, необходимо знать направление света, которое также представляется в виде вектора. Это помогает определить, на каких частях объекта будут находиться тени, а какие — освещены.
Навигация и география — еще одна область, где векторы играют важную роль. Векторы помогают описывать направления и расстояния между объектами на карте или в реальном пространстве, что важно для точной ориентации и прокладки маршрутов.
Пример: GPS-навигация
В системе GPS для определения местоположения объектов и направления движения используются векторы. Векторы помогают вычислять кратчайший путь между двумя точками на земной поверхности, указывая направление движения и расстояние до конечной точки.
Пример: Ветровые потоки и морские течения
Метеорологи и океанографы также используют векторы для описания направлений ветра и морских течений. Каждый поток можно представить в виде вектора, указывающего направление и скорость движения. Это позволяет более точно прогнозировать погодные условия или маршруты движения кораблей.
Где и зачем школьники используют векторы?
Школьники используют векторы в различных учебных дисциплинах, особенно в математике и физике. Вот несколько способов, как они применяют векторы в учебе:
-
Математика:
Векторы изучаются как один из ключевых элементов алгебры и геометрии. Школьники учатся определять направление и длину векторов, складывать их и умножать на скаляр. Это помогает развивать навыки абстрактного мышления и решать задачи, связанные с движением или силами в пространстве. Например, задачи на нахождение длины диагонали квадрата или параллелограмма решаются с помощью применения векторных методов. -
Физика:
Векторы играют важную роль в понимании физических процессов. Школьники изучают, как силы, скорости и ускорения описываются с помощью векторов. Например, чтобы рассчитать результирующую силу, действующую на тело, необходимо сложить несколько векторов сил. Векторное представление величин позволяет лучше понимать динамику движения, работу и энергию. -
Компьютерная графика и программирование:
В современных школах также вводятся основы программирования, где векторы могут использоваться для описания движений объектов в двумерном или трехмерном пространстве. Например, школьники, изучающие простые программы для создания игр, могут применять векторы для расчета перемещения персонажей, их скорости и направления движения.
Таким образом, векторы помогают школьникам не только решать конкретные задачи, но и лучше понимать различные аспекты мира, используя математические и физические модели.
Посмотреть еще в категории: Векторы на плоскости
Посмотреть еще в категории: Векторы на плоскости