Задачи на движение в одном направлении
Рассматриваем, как решать задачи на движение в одном направлении. Представляем алгоритм и способы решения (арифметические и алгебраические).
Задачи на движение в одном направлении и их суть
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Чтобы найти скорость сближения при движении в одном направлении, нужно из большей скорости вычесть меньшую.
Например, если два пешехода отправятся из одного и того же пункта в одном направлении, причем скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 6-4, то есть 2 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиться на 2 километров.
Алгоритм решения задач на движение в одном направлении
Алгоритм и способы решения задач на движение в одном направлении:
- Составляем краткую запись.
- Выбираем способ решения и решаем задачу.
- Выписываем ответ.
Способы решения задач на движение в одном направлении
Задача 1. Из города А в город В вышел поезд со скоростью 50 км/ч. Через 12 ч из того же города вслед поезду вылетел вертолёт, скорость которого в 7 раз больше скорости поезда, и догнал поезд на половине пути от А В. Определи расстояние между городами.
Краткая запись:
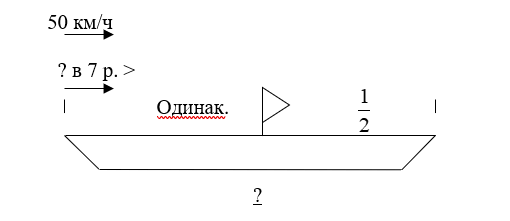
Решение задачи 1:
Арифметические способы решения задачи:
I способ
- Т.к. скорость вертолёта в 7 раз больше, чем скорость поезда, то при одинаковом расстоянии поезд затратит в 7 раз больше времени, чем вертолёт. Значит, время, затраченное поездом, состоит из 7 частей, а время, затраченное вертолётом, состоит из 1 части.
- 7 – 1 = 6 (частей) – на столько частей больше составляет время, затраченное поездом (а поезд был в пути на 12 ч дольше, чем вертолёт).
- 12 : 6 = 2 (часа) – 1 часть (столько был в пути вертолёт).
- 12 + 2 = 14 (ч) – время в пути поезда.
- 50 × 14 = 700 (км) – путь до встречи поезда (половина пути).
- 700 × 2 = 1400 (км) – расстояние между городами.
II способ
- С 1 по 2 действия как в I способе.
- 50 × 7 = 350 (км/ч) – скорость вертолёта.
- 350 × 2 = 700 (км) – путь до встречи вертолёта (половина пути).
- 700 × 2 = 1400 (км) – расстояние между городами.
III способ
- С 1 по 2 действия как в I способе.
- 12 + 2 = 14 (ч) – время в пути поезда.
- 14 × 2 = 28 (ч) – было бы время в пути поезда и вертолёта при равной скорости (50 км/ч).
- 50 × 28 = 1400 (км) – расстояние между городами.
IV способ
- С 1 по 2 действия как в I способе.
- 50 × 7 = 350 (км/ч) – скорость вертолёта.
- 2 × 2 = 4 (ч) – было бы время в пути поезда и вертолёта при равной скорости (350 км/ч).
- 350 × 4 = 1400 (км) – расстояние между городами.
V способ
- С 1 по 2 действия как в I способе.
- 50 × 7 = 350 (км/ч) – скорость вертолёта.
- 350 + 50 = 400 (км/ч) – две скорости.
- 400 : 2 = 200 (км/ч) – средняя скорость.
- 200 × 7 = 1400 (км) – расстояние между городами.
VI способ
- С 1 по 2 действия как в I способе.
- 1 + 7 = 8 (частей) – соответствуют общей скорости.
- 50 × 8 = 400 (км/ч) – две скорости.
- 400 : 2 = 200 (км/ч) – средняя скорость.
- 200 × 7 = 1400 (км) – расстояние между городами.
Алгебраические способы решения задачи:
I способ

Пусть х (ч) – время полёта вертолёта до встречи.
Тогда (12 + х) (ч) – время движения поезда до встречи.
Поезд до встречи прошёл 50 × (12 + х) (км).
Вертолёт до встречи пролетел 50 × 7 × х (км).
По условию задачи эти расстояния одинаковые.
Получится уравнение: 50 × (12 + х) = 50 × 7 ×х.
II способ

Пусть у (ч) – время движения поезда до встречи.
Тогда (у – 12 ) (ч) – время полёта вертолёта до встречи.
Поезд до встречи прошёл 50у (км).
Вертолёт до встречи пролетел 50 × 7 × (у – 12) (км).
По условию задачи эти расстояния одинаковые.
Получится уравнение: 50у = 50 × 7 ×(у – 12).
III способ
Пусть а (ч) – время полёта вертолёта до встречи.
Тогда (12 + а) (ч) – время движения поезда до встречи.
Поезд был в пути дольше, чем вертолёт, в (12 + а) : а раз.
По условию задачи поезд был в пути дольше, чем вертолёт, в 7 раз (т.к. скорость вертолёта в 7 раз больше, чем скорость поезда, то при одинаковом расстоянии поезд затратит в 7 раз больше времени, чем вертолёт).
Получится уравнение: (12 + а) : а = 7.
IV способ
Пусть b (ч) – время движения поезда до встречи.
Тогда (b – 12 ) (ч) – время полёта вертолёта до встречи.
Поезд был в пути дольше, чем вертолёт, во столько раз: b: (b – 12).
По условию задачи поезд был в пути дольше, чем вертолёт, в 7 раз.
Получится уравнение: b: (b – 12) = 7.
Ответ: 1400 км – расстояние между городами.
Посмотреть еще в категории: Задачи на движение
Посмотреть еще в категории: Задачи на движение
